Doctoral Thesis

Lagrangian Methods for Time-dependent Vector Fields

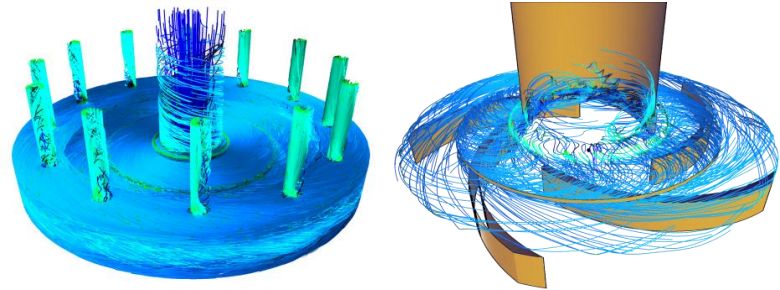
Time-dependent vector fields are of high relevance to describe a wide range of physical phenomena based on particle motion. Such phenomena are stall effects in technical engineering, blood flow anomalies, and atmospheric mass transport. The efficient analysis and fundamental understanding of intrinsic field properties can lead to significant improvements when interacting with such phenomena based on the available data. So called Lagrangian methods are a particularly established technique for this purpose and are based on the evaluation of time-dependent particle trajectories.

This work will present an overview of the state of the art in time-dependent vector field analysis and visualization, with special focus on topology-oriented and Lagrangian methods. The first core aspect of this work is the introduction of a novel concept for a more objective and qualitative benchmark of existing Lagrangian approaches. Based on this benchmark, this work contributes and evaluates a set of novel concepts, which offer new perspectives towards established approaches with respect to computational handling, quality and efficiency of the Lagrangian evluation. The second core aspect is the empirical application and validation of Lagrangian methods with respect to practically relevant analysis scenarios.

Full document link: Lagrangian Methods for Time-dependent Vector Fields